Introducción al Machine Learning

¡Machine Learning!. En resumidas cuentas, es el uso de estadística en forma automatizada para identificar patrones en grandes volúmenes de datos.

Dicho así suena poco emocionante, pero en la práctica el machine learning (de aquí en más ML) ha revolucionado unos cuantos campos debido a su creciente facilidad de uso y a su capacidad -en ciertos contextos- para predecir resultados con alta precisión.

Aquí mostraremos un ejemplo paso a paso de aplicación a un problema relativamente simple, un caso de clasificación binaria: sabiendo que los elementos de un grupo pertenecen a una u otra de dos categorías posibles, encontrar un método para identificar el grupo que les corresponde.

En base a los atributos de un conjunto de propiedades inmobiliarias (valor del metro cuadrado, cantidad de dormitorios, año de construcción, etc) vamos a aplicar ML para predecir si la propiedad se encuentra en Nueva York o en San Francisco.

Una introducción visual al machine learning

Nuestro ejercicio usa los mismos datos y algoritmos que la excelente introducción visual al machine learning. Así que vale la pena revisarla antes de resolver los pasos siguientes, que serían su complemento en versión práctica :)

Paquetes de funciones y datos a utilizar

Haremos uso de los paquetes:

tidyverse, que aporta herramientas para realizar análisis y visualización de datos,
GGally que realiza de forma fácil gráficos con comparación entre variables,
randomForest que provee las funciones para emplear el algoritmo de ML conocido como “Bosques Aleatorios”, o Random Forests, y
caret, una colección de funciones para simplificar el proceso de realizar modelos de ML (sólo vamos a usar una para nuestro ejercicio, pero ofrece muchísimas)

Si aún no contamos con alguno de estos paquetes, los instalamos antes con install.packages(tidyverse), install.packages(RandomForest), etc.

library(tidyverse)
library(GGally)
library(randomForest)
library(caret)

Cargamos también los datos: los precios de propiedades en las ciudades de Nueva York y San Francisco, recopilados por los autores de Una introducción visual al machine learning.

propiedades <- read_csv("https://bitsandbricks.github.io/data/visual_intro_machine_learning.csv")

Paso 0: Definir el problema a resolver

¿Para que necesitamos desarrollar un modelo de ML? En este caso, la respuesta es simple: para distinguir las viviendas ubicadas en Nueva York de aquellas localizadas en San Francisco, en base a un listado de propiedades con sus atributos como precio, dormitorios, etc.

Tener claro el objetivo nos va a ayudar a entender cuales son las variables que más importancia van a tener para realizar la clasificación, o “predicción” que nuestro modelo será capaz de realizar.

Paso 1: Explorar de los datos

Revisemos las variables disponibles:

propiedades

## # A tibble: 492 × 8
##    in_sf  beds  bath   price year_built  sqft price_per_sqft elevation
##    <dbl> <dbl> <dbl>   <dbl>      <dbl> <dbl>          <dbl>     <dbl>
##  1     0     2     1  999000       1960  1000            999        10
##  2     0     2     2 2750000       2006  1418           1939         0
##  3     0     2     2 1350000       1900  2150            628         9
##  4     0     1     1  629000       1903   500           1258         9
##  5     0     0     1  439000       1930   500            878        10
##  6     0     0     1  439000       1930   500            878        10
##  7     0     1     1  475000       1920   500            950        10
##  8     0     1     1  975000       1930   900           1083        10
##  9     0     1     1  975000       1930   900           1083        12
## 10     0     2     1 1895000       1921  1000           1895        12
## # … with 482 more rows

El dataset es sencillo. Sólo 8 columnas, 492 filas. Ningún valor faltante, a primera vista ningún valor extraño o evidentemente erróneo (lo podemos verificar con summary(propiedades)). En la vida real, rara vez encontraremos un dataset tan poco problemático. En general, es inevitable tener que pasar un buen rato entendiendo los datos y tomando decisiones difíciles para corregir ausencia de datos o valores no confiables. ¡Alegrémonos entonces de tener un dataset tan amable para practicar!

La primera columna, “in_sf”, indica si una propiedad se encuentra en San Francisco. Es una variable dicotómica: puede valer “1”, indicando que se encuentra en San Francisco, o “0”, implicando que la vivienda se encuentra en Nueva York. Sólo con fines ilustrativos, vamos a convertir esa variable dicotómica en categórica (es decir, haciendo explícitos los valores “San Francisco” y “New York”).

# creamos una variable categórica que va a quedar más clara en las visualizaciones
propiedades <- propiedades %>% 
  mutate(city = ifelse(in_sf, "San Francisco", "New York")) %>% 
  select(-in_sf) # ya no necesitamos esta variable, porque está representada por "city"

Las demás columnas representan atributos de las propiedades: cantidad de dormitorios, de baños, precio (en dólares), año de construcción, superficie (en pies cuadrados), precio por pie cuadrado, y elevación.

Sabiendo que San Francisco es famosa por sus calles empinadas (lo cual sugiere terreno montañoso, o al menos elevado), imaginamos que el atributo “elevation” va a ser un buen predictor para nuestro modelo.

Realizando una inspección visual, notamos que todas las propiedades en Nueva York aparecen debajo de la línea de 75 metros (la más alta alcanza los 73 metros), mientras que en San Francisco llegan a superar los 225 metros.

ggplot(propiedades) +
    geom_point(aes(x = city, y = elevation, color = city), alpha = 0.3) +
    scale_color_manual(values = c("San Francisco" = "chartreuse4", "New York" = "dodgerblue4")) +
    theme_minimal() +
    guides(color = "none")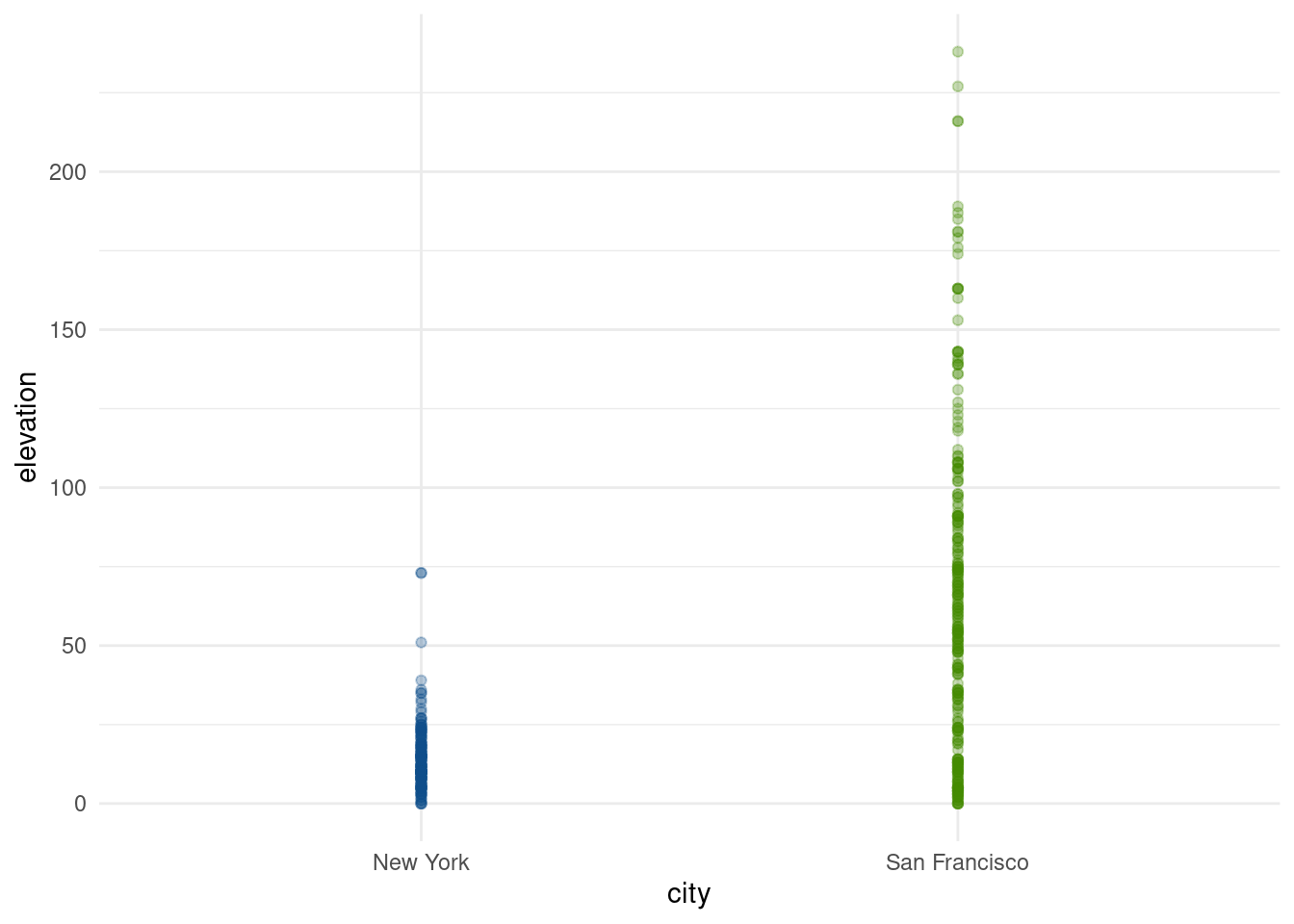

También podemos recordar que Nueva York, como principal centro financiero del mundo, tiene fama de ser un lugar muy caro para vivir… incluso más que San Francisco, que como capital no oficial de Silicon Valley no se queda muy atrás.

Veamos:

ggplot(propiedades) +
    geom_point(aes(x = price_per_sqft, y = elevation, color = city), alpha = 0.3) +
    scale_color_manual(values = c("San Francisco" = "chartreuse4", "New York" = "dodgerblue4")) +
    theme_minimal() +
    guides(color = "none")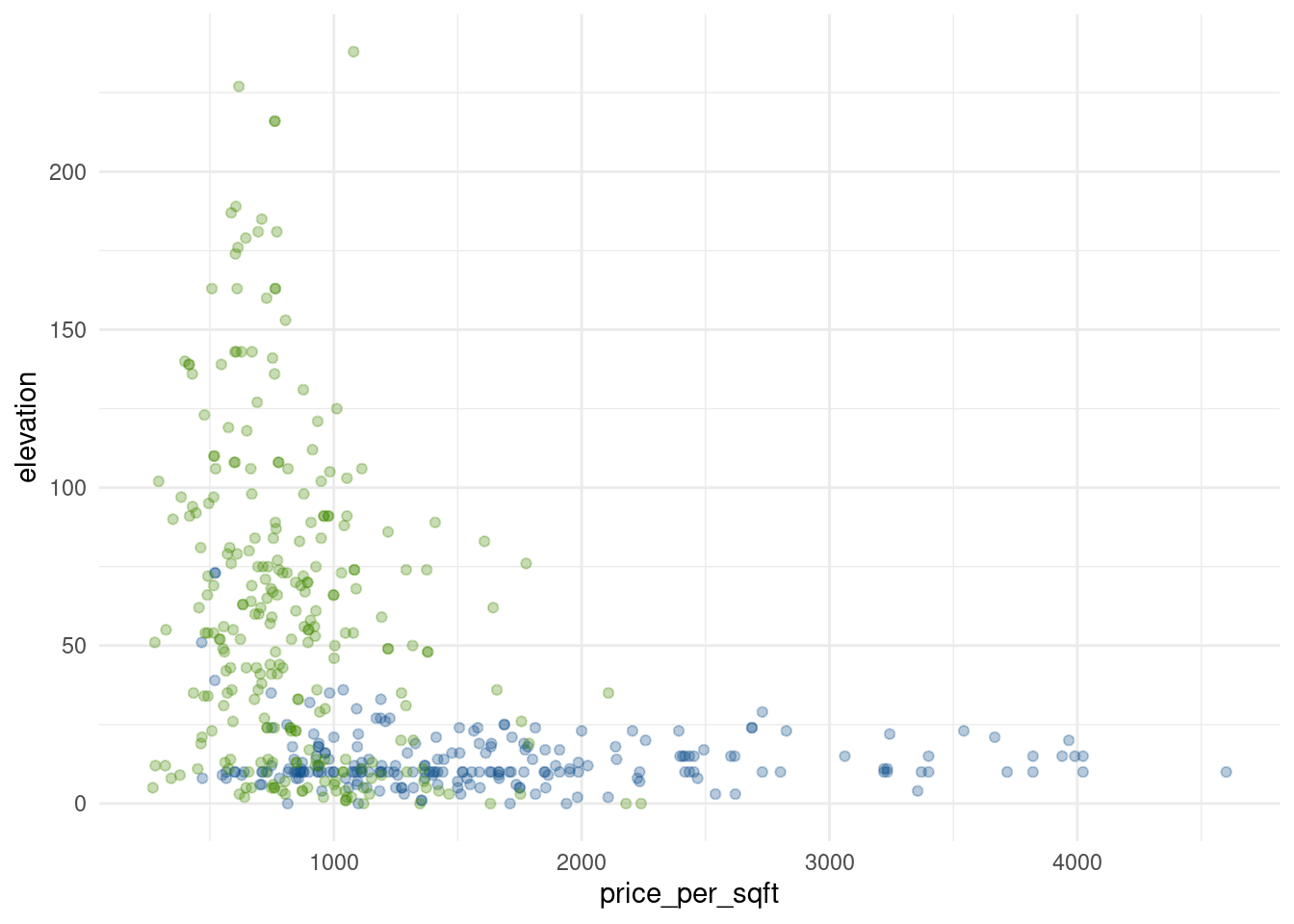

Así como ninguna propiedad en Nueva York se alza más de 73 metros, ninguna en San Francisco presenta un valor por pie cuadrado más allá de la línea que representa 2500 USD (el máximo alcanzado es 2240).

Hemos encontrado otro umbral clave para separar entre las clases “Nueva York” y “San Francisco”. Estos patrones en los datos son clave para los algoritmos de machine learning, ya que en todas sus formas aplican técnicas estadísticas para identificarlos y emplearlos para predecir resultados.

Si comparamos la relación entre todos los pares de variables podemos intuir que hay muchos patrones más, pero ya no son tan evidentes:

ggpairs(propiedades, columns = 2:8, mapping = aes(color = city, alpha = 0.3)) +
  scale_color_manual(values = c("San Francisco" = "chartreuse4", "New York" = "dodgerblue4")) +
  scale_fill_manual(values = c("San Francisco" = "chartreuse4", "New York" = "dodgerblue4")) +
  theme_minimal()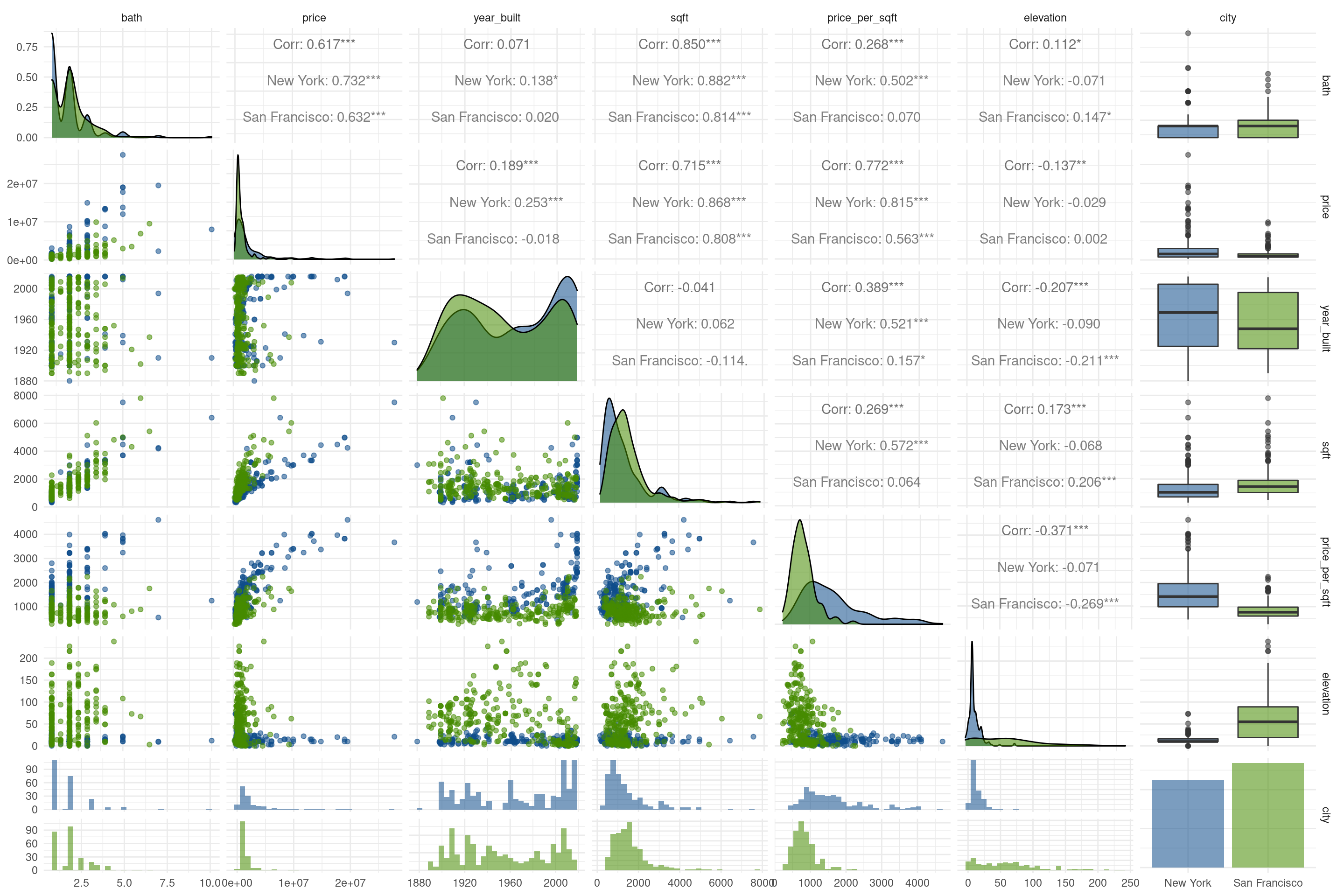

Por suerte, discernir estos patrones no es problema para nuestros cansados ojos. Vamos a dejarlo en manos del algoritmo de ML, o como también le llaman, “aprendizaje estadístico”. Tal como en el ejemplo visual, emplearemos random forest, un algoritmo ideal para empezar: es sencillo de comprender, obtiene buenos resultados, y hasta se deja interpretar. Esto último es algo a resaltar, ya que muchas técnicas de ML resultan en modelos efectivos, pero que no permiten comprender con facilidad cuáles son los atributos en los datos que permiten hacer predicciones.

Paso 2: Preparar los datos

Imputar valores faltantes

Es habitual que los algoritmos empleados para ML no acepten datos faltantes. Al mismo tiempo, sería un desperdicio descartar aquellas filas que tienen algún atributo faltante (por ejemplo, si faltara la cantidad de baños) dado que aún contienen información valiosa en sus campos presentes. Es por eso que la preparación de los datos incluye la imputación de datos no disponibles.

Nuestro dataset amigable no sufre de datos faltantes, pero si los hubiera podríamos imputarlos (asignarles valores asumidos) usando alguna de las muchas técnicas que existen. La más simple es la de valores medios: donde haya un valor desconocido, se reemplaza por el promedio o la mediana de los valores de esa columna.

Codificar variables categóricas

También hay que prestar atención a las variables categóricas, aquí representadas por “city”. Rara vez es posible utilizar columnas categóricas com predictores en modelos estadísticos, pero por suerte podemos recurrir a la alternativa de reemplazar una columna de datos categóricos por una serie de variables dicotómicas, o dummy variables.

Por otro lado, suele ser posible utilizar valores categóricos como variable a predecir. Ese es nuestro caso, ya que buscamos clasificar cada propiedad con una etiqueta que indique “New York” o “San Francisco”. Nos aseguramos de que la variable “city” sea interpretada como categoría, o factor, asignándole el tipo correcto:

propiedades <- propiedades %>% 
  mutate(city = as.factor(city))

Unificar la escala de las variables numéricas

Éste paso siempre es necesario cuando estamos trabajando con variables que utilizan distintas unidades de medida. Aquí tenemos elevaciones, cantidad de dormitorios, años de antigüedad… de todo. Muchos algoritmos asumen que todas las variables tienen escalas comparables, lo cual genera problemas con las que alcanzan valores relativamente muy altos (como precio, que llegar a millones) versus las que tienen rangos mucho menores (como año de construcción, que sólo llega a 2016). Si las dejásemos así, varias de las técnicas habituales del ML adjudicarían mucho más peso a las variables con números grandes, despreciando a las que por su naturaleza se mueven en rango más reducidos.

En todo caso, no importa lo disimiles que sean las unidades de medida, la solución es simple: convertimos todas las variables a la famosa escala de “valores Z” con la función de estandarización, que convierte variables a una escala sin unidad de medida que expresa cada valor como la cantidad de desvíos estándar que lo alejan de la media. Expresar todas las variables numéricas en forma de Z-scores, o " valores Z" las hace directamente comparables entre sí.

En R disponemos de la función scale(), que obtiene los Z-scores. Tomaremos entonces nuestro dataframe y usaremos mutate() en combinación con across() para aplicar la función a varias columnas de un tirón. Algunas variables no necesitan ser transformadas: las variables categóricas (que no tiene sentido pasar a Z-scores porque no son variables numéricas), y la variable que estamos intentando predecir, ya que su escala no afecta los modelos y podemos dejarla en su formato original.

propiedades_Z <- propiedades %>%
  mutate(across(beds:elevation, scale)) # aquí aplicamos la función scale a las columnas de "bed" a "elevation"

Podemos ver que, tras la transformación,las variables que usaremos como predictores están centradas en 0, y tienen rangos similares.

propiedades_Z %>% 
  pivot_longer(cols = beds:elevation) %>% 
  ggplot() +
    geom_histogram(aes(x = value, fill = city), position = "dodge") +
    scale_fill_manual(values = c("San Francisco" = "chartreuse4", "New York" = "dodgerblue4")) +
    facet_wrap(~name) +
    guides(fill = "none") +
    theme_minimal() +
    labs(title = "Valores transformados a Z-scores")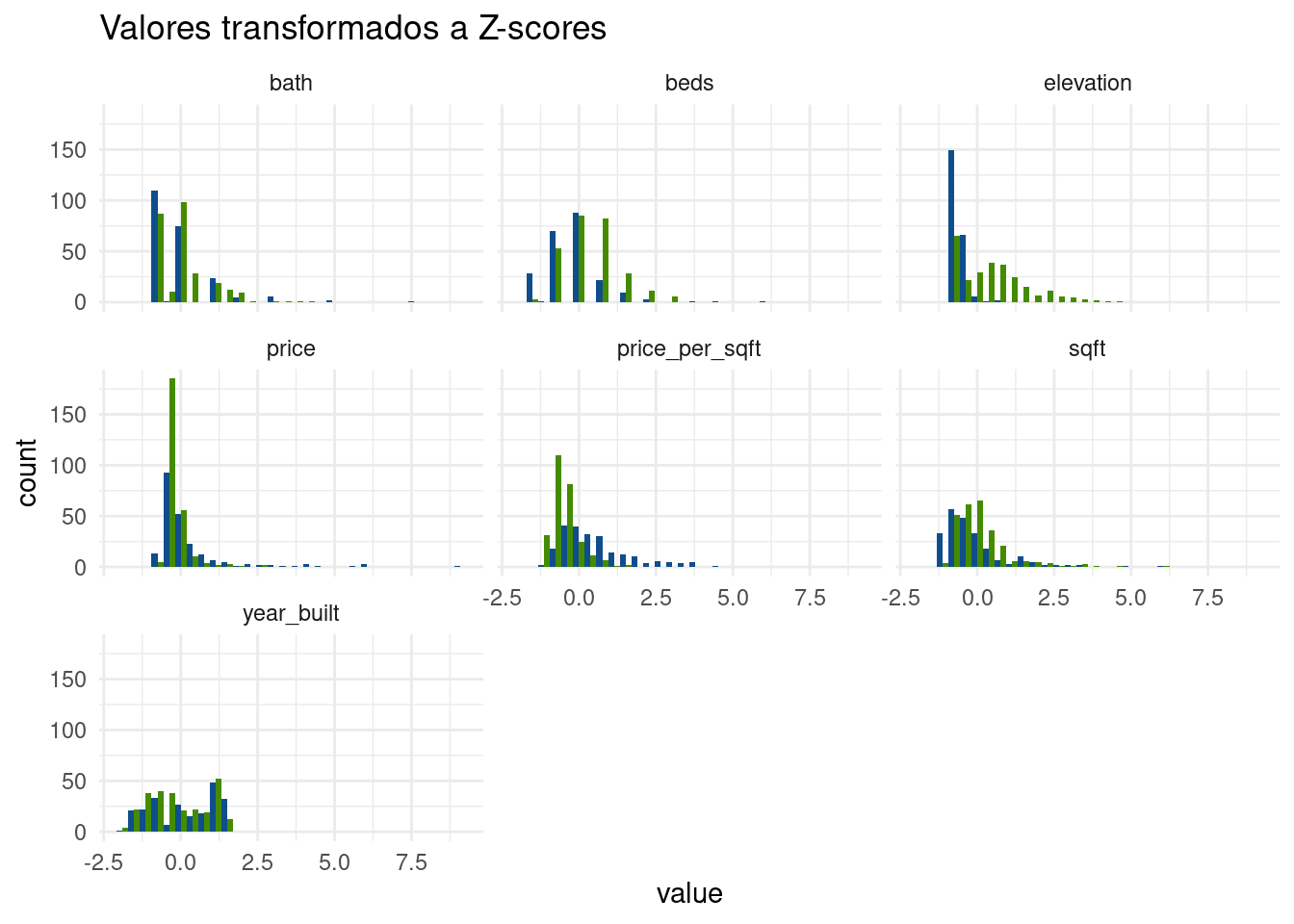

Al realizar la transformación hemos eliminado las unidades de medida (pies cuadrados, metros, dólares), y con eso hemos dejado a las variables entre si. Y todo sin perder la forma original de las distribuciones. Esto es clave, la distancia relativa entre valores sigue siendo la misma. Es decir, si una propiedad que vale tres veces más que otra, se conserva esa proporción cuando se expresan los valores como Z-scores.

Paso 3: Crear sets de entrenamiento y de testeo

Para poder evaluar la calidad de un modelo predictivo, es práctica común dividir los datos disponibles en dos porciones:

Una parte será utilizada para “entrenar” el modelo de ML, es decir se le permitirá al algoritmo acceder a esos datos para establecer la forma en que cada variable predictora incide en la que se quiere predecir.
El resto será preservado y utilizado para “tomarle examen” al modelo: se le mostraran sólo las variables predictoras de esos datos, pidiendo al modelo una predicción del valor a estimar para cada una. Por último, contrastando aciertos y errores, se podrá establecer el grado de precisión del modelo.

Incluso podríamos tener varios modelos distintos, obtenidos con distintas técnicas de ML. No es difícil, ya que una vez que los datos han sido obtenidos y preparados, nada impide usarlos como insumo de distintos algoritmos. En ese caso, se puede comparar la performance de los distintos modelos evaluando cual acierta mejor con la data de testeo.

Definamos entonces cuales filas van al set de entrenamiento, y cuáles al de testeo, eligiéndolas al azar. De acuerdo a distintas recetas, a veces se separa el 90% de los datos para entrenamiento y el resto para testeo, otras veces es mitad y mitad… ya que siempre es más o menos arbitrario, aquí seguiremos el ejemplo de Introducción visual… y repartiremos los datos como mitad para entrenamiento y mitad para testeo.

# definimos a mano la "semilla" de aleatorización para obtener resultados reproducibles
set.seed(1810)

# esta línea elige al azar la mitad de los numeros que van de 1 al total de filas del dataset
seleccion <- sample(1:nrow(propiedades_Z), size = nrow(propiedades_Z) * 0.5)

# Con esto seleccionamos las filas "sorteadas", que van al set de entrenamiento
entrenamiento <- propiedades_Z %>% 
    filter(row_number() %in% seleccion)

# Y con esto elegimos al resto de las filas, que van al set de testeo
# el operador ! convierte una proposición en negativa - aquellas filas cuya posición no está entre las seleccionadas
testeo <- propiedades_Z %>% 
    filter(!(row_number() %in% seleccion))

Paso 4: Entrenar el modelo

Ahora si, a ver esos árboles en acción! El algoritmo random forest se basa en árboles de decisión, que como vimos en la intro visual separa las observaciones en categorías de acuerdo a una serie de comparaciones consecutivas, identificando los puntos de corte que mejor separan entre sí a las categorías que queremos predecir:

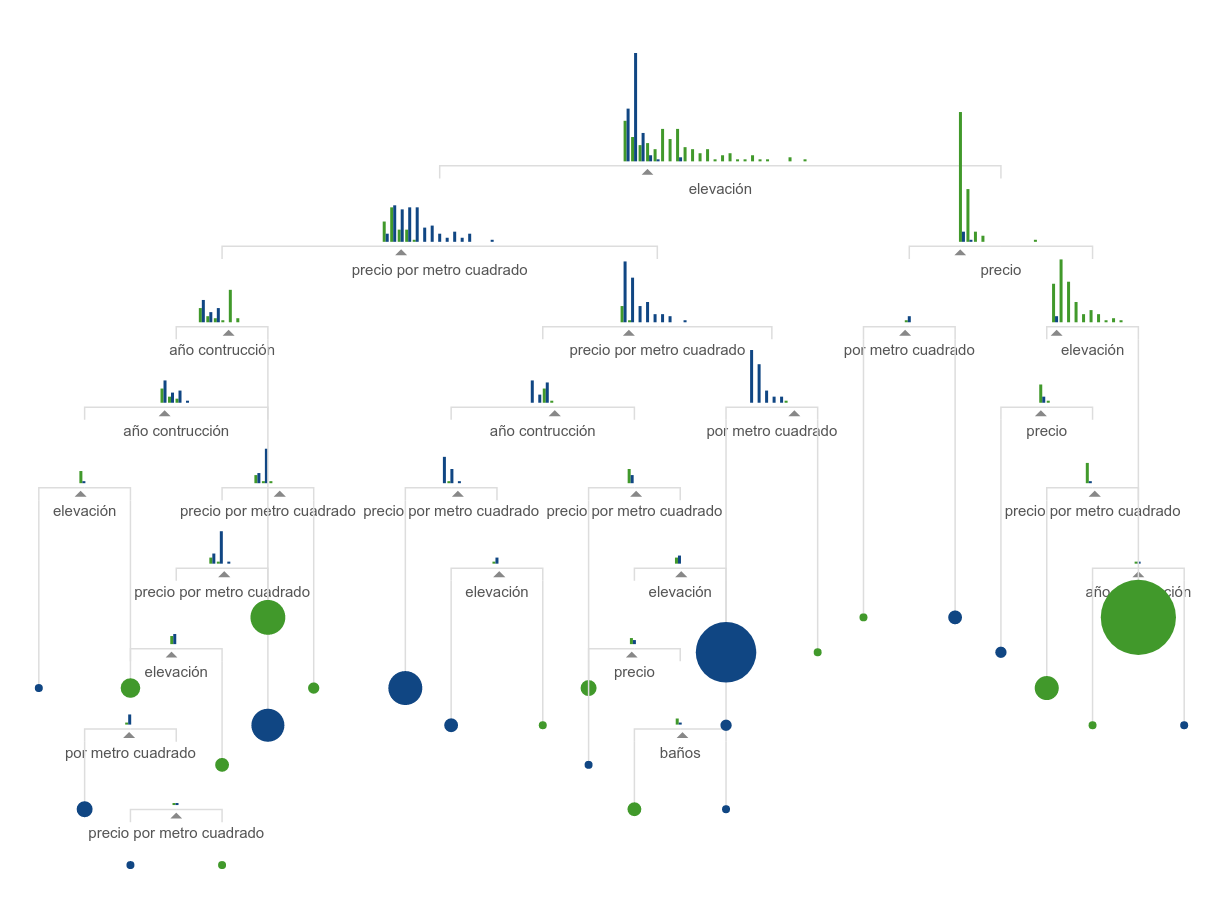
Al usar random forest en verdad producimos unos cuantos árboles de decisión, ligeramente distintos entre si. Las predicciones de cada árbol se usan en una especie de votación, y en base a la mayoría se determina la categoría a la que corresponde cada observación. De allí el “forest”: tenemos un conjunto de árboles. La gracia es que al combinar y sopesar los resultados de múltiples variantes se obtienen mejores predicciones que las un sólo árbol. Es un ejemplo de “ensemble learning”, la combinación de múltiples algoritmos (o de variaciones de un mismo algoritmo) para mejorar la performance predictiva.

Para hacer crecer ese bosque usaremos la función randomForest(). Con lo datos preparados, solo necesitamos indicarle

la variable a predecir y las variables predictoras
el origen de los datos

Como extra opcional, también vamos a especificar

ntree = N, para la cantidad de árboles a calcular,
importance = TRUE, para que el modelo incluya un estimado de la importancia de cada variable para la predicción

randomForest() sólo acepta valores numéricos como predictores. Si tuviéramos variables categóricas para predecir, sería cuestión de convertirlas en dicotómicas, o “dummy” (re-expresadas en valores de 1 o 0, como vimos al principio para el campo “in_sf”) y con eso podríamos continuar.

Como variable a predecir, la función acepta una de tipo numérico (en cuyo caso hace un modelo de regresión) o categórico, en cuyo caso hace un modelo de clasificación.

Recordemos que en la notación de fórmulas de R el símbolo . significa “todas las demás variables”. O sea, city ~ . equivale a “predecir el valor de ‘city’ usando el resto de las columnas como predictores”

modelo_RF <- randomForest(city ~ .,
                          data = entrenamiento,
                          ntree = 500,
                          importance = TRUE)

¿Qué obtuvimos?

modelo_RF

## 
## Call:
##  randomForest(formula = city ~ ., data = entrenamiento, ntree = 500,      importance = TRUE) 
##                Type of random forest: classification
##                      Number of trees: 500
## No. of variables tried at each split: 2
## 
##         OOB estimate of  error rate: 11.38%
## Confusion matrix:
##               New York San Francisco class.error
## New York           101            11  0.09821429
## San Francisco       17           117  0.12686567

La matriz de confusión, un clásico recurso para evaluar modelos, nos indica la performance del modelo obtenido. Nos resume la cantidad de predicciones correctas, e incorrectas, para cada categoría al aplicar el modelo a los datos que usamos para entrenarlo. En las columnas aparece el valor predicho, en las filas el valor real.

¿Qué más tiene dentro el modelo?

summary(modelo_RF)

##                 Length Class  Mode     
## call               5   -none- call     
## type               1   -none- character
## predicted        246   factor numeric  
## err.rate        1500   -none- numeric  
## confusion          6   -none- numeric  
## votes            492   matrix numeric  
## oob.times        246   -none- numeric  
## classes            2   -none- character
## importance        28   -none- numeric  
## importanceSD      21   -none- numeric  
## localImportance    0   -none- NULL     
## proximity          0   -none- NULL     
## ntree              1   -none- numeric  
## mtry               1   -none- numeric  
## forest            14   -none- list     
## y                246   factor numeric  
## test               0   -none- NULL     
## inbag              0   -none- NULL     
## terms              3   terms  call

¡De todo!

Por ejemplo, “type” nos permite confirmar qué tipo de análisis realizó: Fue de clasificación en este caso, peor podría haber sido regresión (cuando pedimos predecir un atributo una variable continua, como “precio”, en lugar de un atributo categórico como “ciudad”):

modelo_RF$type

## [1] "classification"

O “importance”, que contiene un ranking con la importancia relativa de cada predictor, es decir cuáles son los que más ayudan a predecir:

modelo_RF$importance

##                  New York San Francisco MeanDecreaseAccuracy MeanDecreaseGini
## beds           0.05620448  0.0202547669           0.03634804         9.157887
## bath           0.02847641 -0.0001771553           0.01262316         3.676089
## price          0.07496220  0.0186997083           0.04429778        13.911648
## year_built     0.03677242  0.0317526190           0.03401093        13.197126
## sqft           0.08462510  0.0278094326           0.05357976        16.074712
## price_per_sqft 0.16516605  0.0492492461           0.10177501        27.843443
## elevation      0.20263756  0.1099576405           0.15115956        37.385107

Las columna con las categorías como nombre expresan en cuánto se incrementa el error clasificación (en porcentaje) cuando el predictor de la fila se retira del modelo (es decir, cuanto peor sería la predicción si no se usara). Por eso los números mayores están asociados a los predictores de más peso, que en este caso son “elevation”, y “price_per_sqft”, como ya habíamos intuido en la exploración de los datos. En tercer lugar -y esto si es revelatorio- aparece la superficie de las propiedades, que ha resultado ser el mejor predictor de ubicación entre las variables que no mostraban un patrón obvio.

La columna MeanDecreaseAccuracy expresa el promedio de error para todas las categorías (las columnas anteriores), si se quitara esa variable predictora. Por su parte, MeanDecreaseGini indica la pérdida promedio de “pureza” en la clasificación de los nodos de los árboles, es decir que tanto más mezcladas quedan las categorías en cada punto de decisión al no contar con la variable predictora; está expresado en índice de impureza de Gini (no confundir con el tradicional coeficiente de Gini).

En “predicted” el modelo guarda su predicción para cada valor con el que fue entrenado. Comparando las predicciones con los valores reales podemos realizar la matriz de confusión que aparece en el resumen del modelo, junto a varias métricas de performance. Aquí nos asiste la función confusionMatrix del paquete caret, y para eso lo hemos cargado al inicio:

confusionMatrix(modelo_RF$predicted, modelo_RF$y)

## Confusion Matrix and Statistics
## 
##                Reference
## Prediction      New York San Francisco
##   New York           101            17
##   San Francisco       11           117
##                                          
##                Accuracy : 0.8862         
##                  95% CI : (0.8397, 0.923)
##     No Information Rate : 0.5447         
##     P-Value [Acc > NIR] : <2e-16         
##                                          
##                   Kappa : 0.7715         
##                                          
##  Mcnemar's Test P-Value : 0.3447         
##                                          
##             Sensitivity : 0.9018         
##             Specificity : 0.8731         
##          Pos Pred Value : 0.8559         
##          Neg Pred Value : 0.9141         
##              Prevalence : 0.4553         
##          Detection Rate : 0.4106         
##    Detection Prevalence : 0.4797         
##       Balanced Accuracy : 0.8875         
##                                          
##        'Positive' Class : New York       
##

Quedémonos por ahora con el valor de “Accuracy”, el porcentaje de predicciones que el modelo acertó: en este caso, algo más de un 88%.

A medida que profundicemos en la práctica del ML, aprenderemos que la accuracy, o “precisión” no cuenta toda la historia, y muchas veces puede ser engañosa. Por ejemplo, cuando las clases no están “balanceadas”, es decir que alguna categoría tiene muy pocas instancias en los datos: aún si todas fueran mal clasificados, ésto no tendría un gran impacto en el valor global de la precisión y así se escondería la mala performance.

¡Pero eso no ocurre aquí! Así que continuemos tranquilos.

Paso 5: Testear el modelo

Ahora vamos a medir la performance del modelo contra datos que no conoce. Lo usaremos para clasificar propiedades que no se han utilizado para su entrenamiento, las que reservamos en el set de testeo. La función predict() permite aplicar un modelo contra un dataset con la misma estructura del que se usó para entrenarlo, y obtener sus predicciones:

predicciones_test <- predict(modelo_RF, newdata = testeo)

Ahora, medimos performance vía matriz de confusión:

confusionMatrix(predicciones_test, testeo$city)

## Confusion Matrix and Statistics
## 
##                Reference
## Prediction      New York San Francisco
##   New York           103            17
##   San Francisco        9           117
##                                          
##                Accuracy : 0.8943         
##                  95% CI : (0.849, 0.9298)
##     No Information Rate : 0.5447         
##     P-Value [Acc > NIR] : <2e-16         
##                                          
##                   Kappa : 0.7882         
##                                          
##  Mcnemar's Test P-Value : 0.1698         
##                                          
##             Sensitivity : 0.9196         
##             Specificity : 0.8731         
##          Pos Pred Value : 0.8583         
##          Neg Pred Value : 0.9286         
##              Prevalence : 0.4553         
##          Detection Rate : 0.4187         
##    Detection Prevalence : 0.4878         
##       Balanced Accuracy : 0.8964         
##                                          
##        'Positive' Class : New York       
##

¡Pasó la prueba! La performance con datos que no conoce es similar, incluso levemente mejor. Nuestro modelo no sufre de sobreajuste u overfitting, el defecto de haberse basado en patrones de los datos de entrenamiento que son irrelevantes para predecir otros casos.

En forma visual:

ggplot() +
  geom_jitter(aes(x = predicciones_test, y = testeo$city, color = testeo$city)) +
  scale_color_manual(values = c("San Francisco" = "chartreuse4", "New York" = "dodgerblue4")) +
  guides(color = "none") +
  labs(x = "categoría correcta",
       y = "categoría predicha")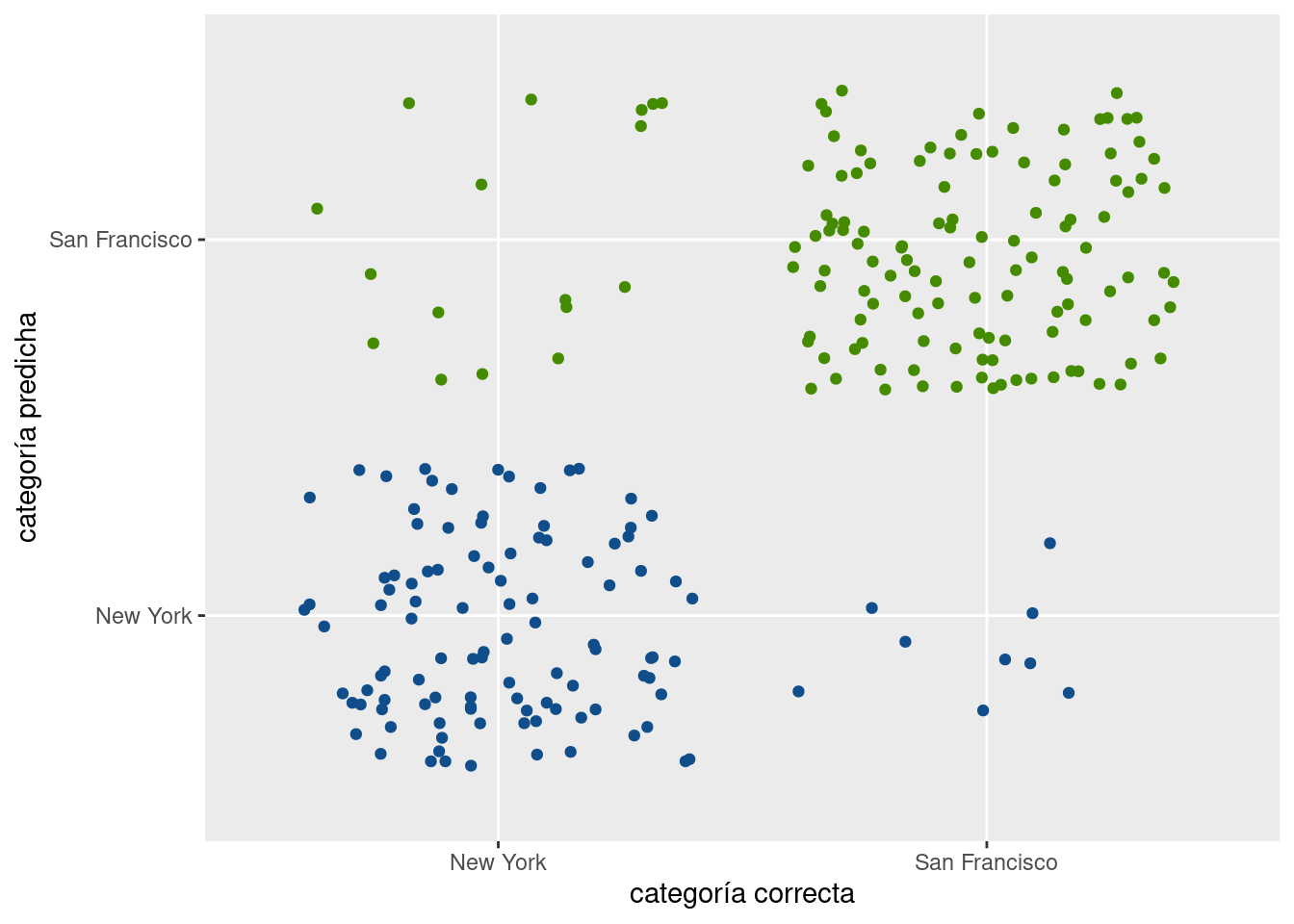

La gran mayoría de las propiedades fue correctamente clasificada (gracias a la matriz de confusión, sabemos que la cantidad es más del 89%).

Para seguir practicando

Ahora queremos usar nuestros datos para predecir una variable continua, como por ejemplo el año de construcción. Entrenamos un nuevo modelo, ésta vez así:

modelo_RF_regresion <- randomForest(year_built ~ .,
                          data = entrenamiento,
                          ntree = 500,
                          importance = TRUE)

Con lo que ya sabemos, podemos responder las siguientes preguntas:

¿Qué tan buenos son los resultados del modelo?
¿Cuáles son los atributos que más contribuyen a predecir el año de construcción?
¿Qué tan buena es la performance cuando se testea al modelo con datos que no “visto” antes?

Y si probamos predecir otra variable continua, como el precio…

¿Los resultados son mejores o peores, respecto al año de construcción?
¿Todas las variables del dataset pueden predecirse con éxito similar?

machinelearning R