DBSCAN: Machine Learning para detectar centros de actividad urbana

DBSCAN es un algoritmo de machine learning diseñado para detectar en forma automática “clusters”, es decir elementos próximos entre si de acuerdo a sus atributos en varias dimensiones.

A diferencia de otros algoritmos de clustering como KMeans, DBSCAN resulta muy adecuado para buscar patrones de agrupación en el espacio físico. Por ejemplo, en la distribución espacial de actividades humanas.

Como se ilustra debajo, entre varias alternativas DBSCAN es la única cuyos resultados aproximan los de un analista humano que estuviera clasificando puntos aglomerados en un mapa:

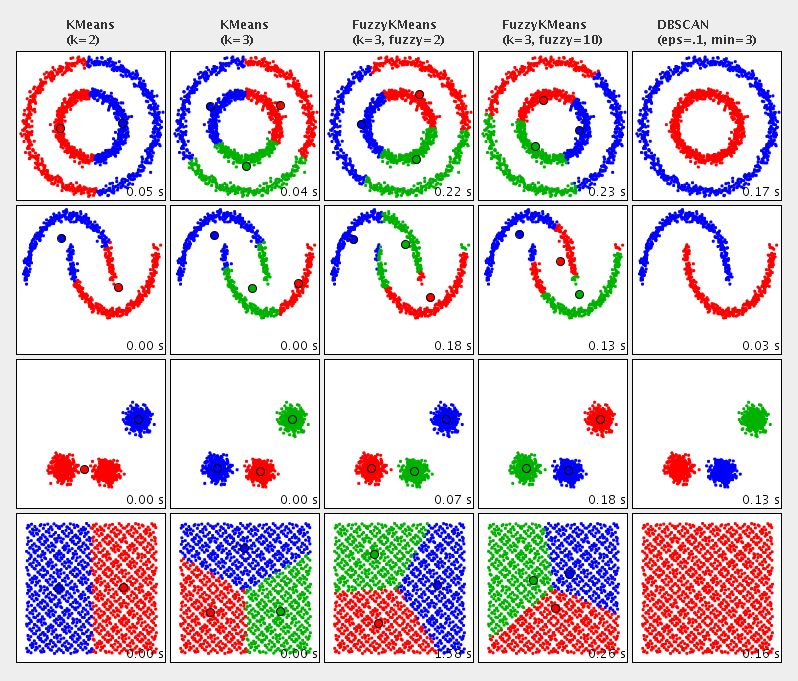(imagen vía hipparchus.org)

Pongámoslo a trabajar entonces, para identificar los centros comerciales (y de otros tipos de actividad) en la ciudad de Mendoza y sus alrededores. Un ejercicio como este, si se repitiera con cierta frecuencia, permitiría detectar la aparición, desplazamiento o desaparición de distintos centros de actividad especializada en la ciudad: zonas con oferta concentrada de bares, de servicios profesionales, de tiendas de bicicletas o lo que fuere.

Paquetes a utilizar

Los herramientas generales de Tidyverse, siempre útiles para el proceso general de análisis de datos:

library(tidyverse)

y cuatro paquetes especializados:

sf para leer y procesar datos geoespaciales
geosphere para calcular distancias sobre la superficie terrestre
dbscan para emplear el algoritmo homónimo de machine learning que permite encontrar clusters de elementos próximos
ggmap para obtener y visualizar mapas detallados de la ciudad que analizaremos

library(sf)
library(geosphere)
library(dbscan)
library(ggmap)

Los datos

Trabajaremos con un dataset de “puntos de interés”, o PoI en la jerga de aplicaciones espaciales (por “Points of Interest”).

mdz_poi <- read_csv('https://bitsandbricks.github.io/data/mendoza_poi.csv')

head(mdz_poi)

## # A tibble: 6 x 5
##   nombre                                             tipo  categoria   lat   lng
##   <chr>                                              <chr> <chr>     <dbl> <dbl>
## 1 Banco de la Nación Argentina                       atm   banca     -32.9 -68.8
## 2 Hospital Central BANCO DE LA NACION ARGENTINA Caj… atm   banca     -32.9 -68.8
## 3 Banelco                                            atm   banca     -32.9 -68.8
## 4 Banelco                                            atm   banca     -32.9 -68.8
## 5 Cajero Automatico Banelco                          atm   banca     -32.9 -68.8
## 6 Citibank                                           bank  banca     -32.9 -68.8

Se trata de lugares en el área urbana de Mendoza, de 93 tipos distintos, agrupados en 12 categorías generales:

count(mdz_poi, categoria, tipo)

## # A tibble: 93 x 3
##    categoria tipo                 n
##    <chr>     <chr>            <int>
##  1 banca     atm                 93
##  2 banca     bank               112
##  3 culto     church             248
##  4 culto     mosque               2
##  5 culto     place_of_worship     4
##  6 culto     synagogue            3
##  7 cultura   art_gallery         14
##  8 cultura   library             18
##  9 cultura   museum              55
## 10 educacion school             890
## # … with 83 more rows

Los datos fueron compilados a mediados del 2017, a partir de consultas a la base de Google Places. Google Places es la base de datos donde Google registra información sobre puntos de interés (comercios, prestadores de servicios, terminales de transporte y un largo etcétera) en cualquier parte del mundo. La forma habitual de acceder a partes de esta información es mediante la Google Maps, desde un navegador o una app de smartphone, pero también es posible consultar la base de forma automatizada, el modo con el cual se relevaron las datos que estamos usando.

Implementando DBSCAN

Para practicar, empecemos por detectar clusters de bares.

I. Realizar una matriz de distancias

El primer paso para aplicar el algoritmo es obtener una matriz con la distancia que media entre todos los puntos a analizar. Dado que trabajamos con lugares situados sobre la superficie terrestre, debemos calcular distancias geográficas; es decir, tomar en cuenta la curvatura de la superficie. Para ellos podemos usar la función distm() del paquete geosphere.

Veamos como lucen nuestros bares en el mapa:

mdz_bares <- mdz_poi %>% 
    filter(tipo == "bar")

# Definir la "caja" de coordenadas donde entran los datos, para luego pedir el mapa
bbox <- c(min(mdz_poi$lng),
          min(mdz_poi$lat),
          max(mdz_poi$lng),
          max(mdz_poi$lat))

mendoza <- get_stamenmap(bbox = bbox, maptype = "toner-background", zoom = 13)


ggmap(mendoza) +
    geom_point(data = mdz_bares, aes(x = lng, y = lat), color = "orange", alpha = .5)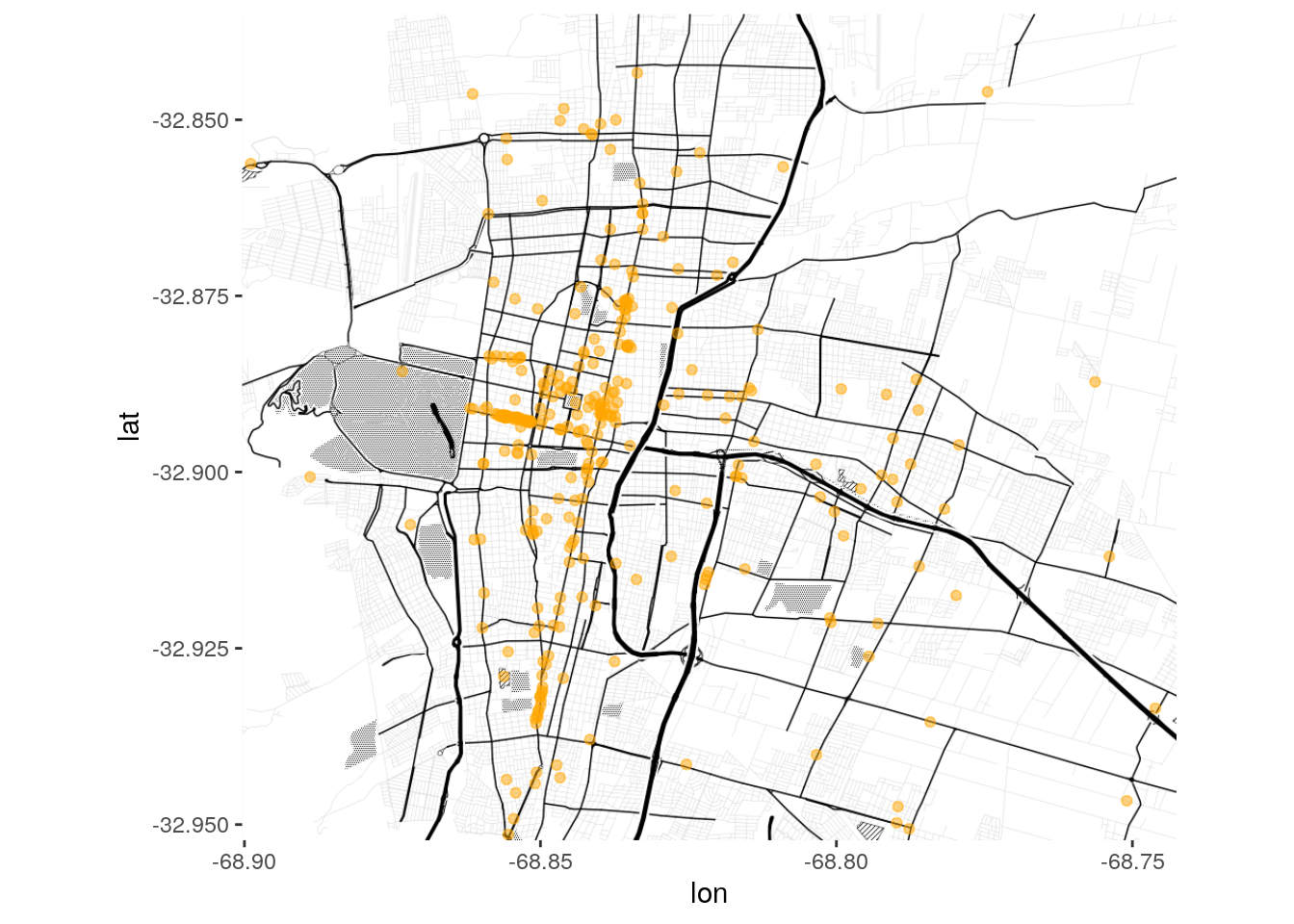

Ahora creamos la matriz con la distancia entre cada par de puntos (es decir, medimos la distancia de cada bar contra todos los demás), el insumo que requiere DBSCAN.

distancias <- mdz_bares %>%
    select(lng, lat) %>% # extraemos las columnas de longitud y latitud
    distm(fun = distGeo) %>% # Calculamos las distancias de acuerdo a la curvatura de la Tierra
    as.dist() # convertimos en una matriz de distancias (el tipo de objeto que DBSCAN espera)

II. Definir parámetros

Con la matriz de distancias a mano, es hora de decisiones. Tenemos que fijar dos parámetros, con el fin de identificar zonas densas, medidas por la cantidad de objetos cercanos a cualquier punto dado:

epsilon es el radio de “vecindad” en torno a un punto.
minPts es la cantidad mínima de vecinos dentro del radio epsilon que alcanzan para definir a ese punto como miembro de un cluster

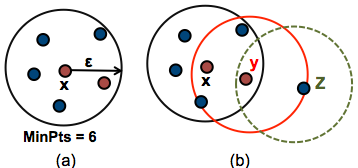(fuente aquí)

En (a) vemos a x, un punto “núcleo”(core). Son puntos “núcleo” aquellos que dentro de su radio epsilon tienen la cantidad mínima de vecinos definida como minPts. En (b) vemos también a y y a z. y es un punto “borde” porque su cantidad de vecinos es menor a minPts, pero de todas formas se encuentra en la vecindad de un punto núcleo. Los puntos núcleo y borde que comparten vecindad son parte del mismo cluster. z es considerado “ruido” ya que no es núcleo ni borde, y por tanto no pertenece a un cluster.

Ahora bien, ¿cómo decidimos que cantidad es buena para minPts, y que distancia para epsilon? No hay receta infalible. Depende de cada caso, y se pueden encontrar por prueba y error. Para nuestro problema, decidámoslo así: vamos a considerar como cluster aquellas zonas donde, en un radio de una cuadra (128 metros) a la redonda de un bar dado, se encuentren al menos otros 5 bares. Tendremos entonces epsilon = 128 y minPts = 5.

III. Aplicar el algoritmo

Allá vamos:

clusters <- dbscan(distancias, eps = 128, minPts = 5)

clusters

## DBSCAN clustering for 321 objects.
## Parameters: eps = 128, minPts = 5
## The clustering contains 9 cluster(s) and 207 noise points.
## 
##   0   1   2   3   4   5   6   7   8   9 
## 207   8  43   6   6  22   6  12   6   5 
## 
## Available fields: cluster, eps, minPts

Con nuestras reglas, encontramos 9 clusters en la ciudad. Los bares cuyo valor asignado es 0 son “ruido”, los que no pertenecen a ningún cluster.

IV. Visualizar los resultados

Agreguemos a cada bar el cluster que le corresponde:

mdz_bares <- mdz_bares%>% 
    cbind(cluster = clusters[["cluster"]])

Y con eso a podemos proyectar los resultados en un mapa:

# Visualizamos en un capa los bares sin cluster, y luego los que estan agrupados en otra
ggmap(mendoza) +
    geom_point(data = filter(mdz_bares, cluster == 0), 
               aes(x = lng, y = lat), 
               alpha = .5) +
    geom_point(data = filter(mdz_bares, cluster > 0), 
               aes(x = lng, y = lat, color = factor(cluster)), 
               alpha = .5) +
    labs(title = "Mendoza: clusters de bares",
         color = "cluster")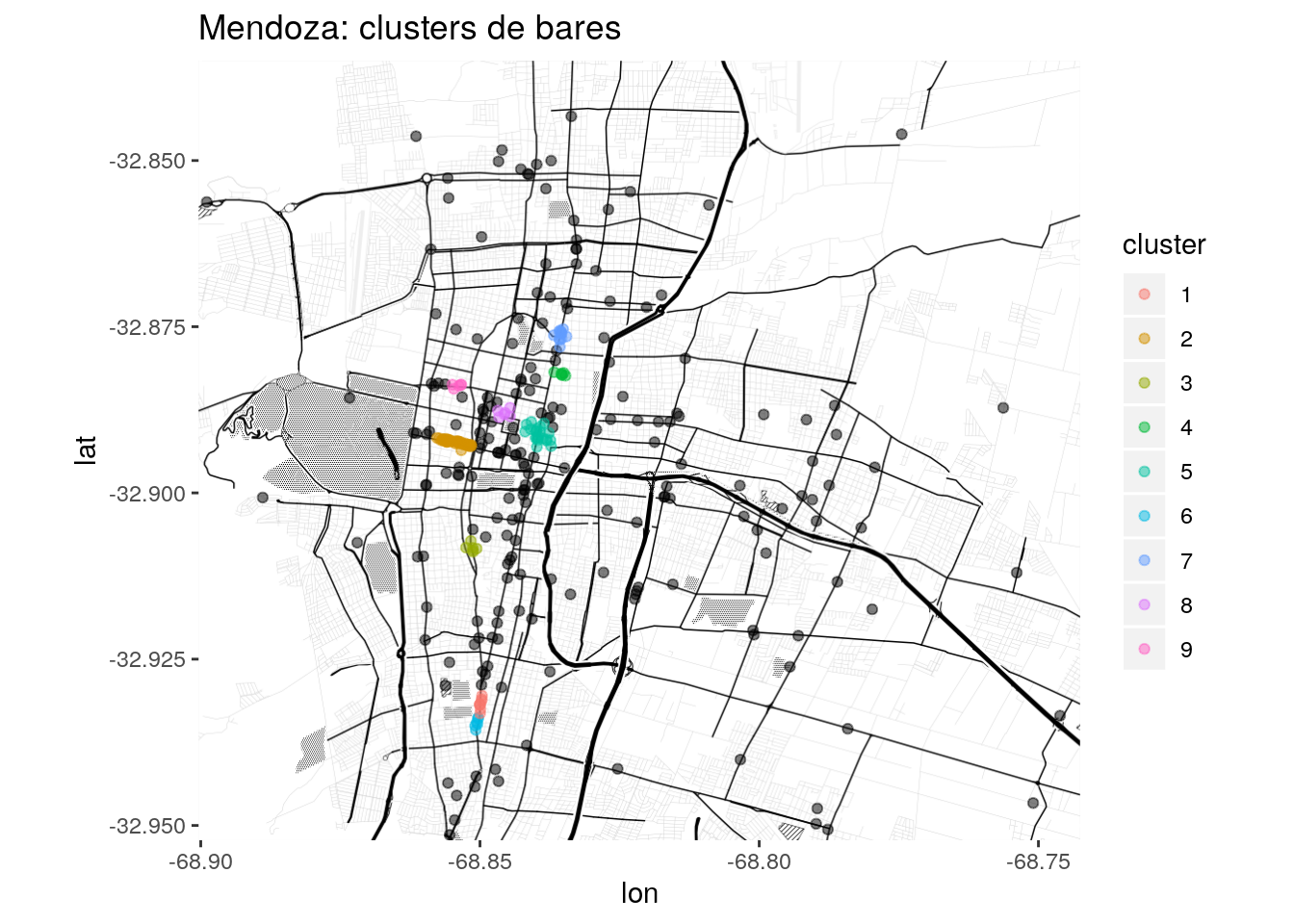

Automatizando la detección

Vamos a crear una función que realice todos los pasos que vimos antes: realizar la matriz de distancia, fijar los parámetros de DBSCAN, aplicar el algoritmo, y agregar los identificadores de cluster a la data original.

Ya que vamos a lidiar con categorías generales (por ejemplo “servicios” incluye de todo, desde dentistas a funerarias) vamos a ponernos exigentes con los parámetros. Consideraremos que un punto pertenece a un cluster de actividad cuando tiene al menos 25 vecinos en una cuadra a la redonda. Con algunas excepciones: para banca, cultura, culto, educación, entretenimiento, espacios_verdes, gobierno_y_serv_publicos y salud, dejaremos en 5 al umbral. Estos son sitios de mayor “peso”. Seis bares en estrecha proximidad no representan una agrupación notable, pero con seis sedes de la administración pública, o seis museos, ya hablaríamos un centro de actividad.

Si bien permite especificar minPts si lo quisiéramos, nuestra función se encargará de verificar el tipo de categoría a la que corresponden los puntos, y fijar el parámetro en forma acorde.

assign_clusters <- function(poi_df, minPts = NA) {
    
    # Para ciertas categorias, como educacion o salud, consideramos que a partir de n = 5 ya se 
    # forma clustering.
    # Para las demas (retail y servicios) el umbral se eleva a 25
    
    if(is.na(minPts)) {
        if(poi_df[1, "categoria"] %in% c("banca", "cultura", "culto", "educacion", "entretenimiento", 
                                         "espacios_verdes", "gobierno_y_serv_publicos", "salud")) {
            minPts <- 5
        } else minPts <- 25
    }
    
    
    eps <- 128 #  metros de distancia máxima entre miembros de un cluster
    
    poi_df[c("lng", "lat")] %>% 
        distm(fun = distHaversine) %>%
        as.dist() %>% 
        dbscan(eps = eps, minPts = minPts) %>% 
        .[["cluster"]] %>% 
        cbind(poi_df, cluster = .)
    
}

Ahora aplicamos la función a nuestros datos.

ATENCION! Con menos de 16 GB de RAM en el sistema, es posible que los recursos no alcancen para procesar el próximo bloque de código. El consumo de memoria de DBSCAN aumenta en forma exponencial (cuadrática) a medida que se incrementan la cantidad de puntos a analizar.

mdz_poi <- mdz_poi %>%
    # separamos el dataset en una lista con un dataframe por cada categoría
    split(mdz_poi$categoria) %>%  
    # Le aplicamos al dataframe de cada categoría la función de clustering
    map_df(assign_clusters)

Listo!

Producto final: un mapa con todos los clusters hallados por categoría

Antes de llevar los resultados al mapa, extraigamos para cada cluster su convex hull.

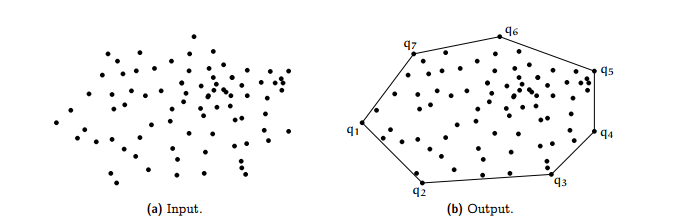(gráfico cortesía de Harshit Sikchi)

La “envolvente convexa” de un cluster no es otra cosa que un polígono que encierra todos sus puntos. La idea es usarlas para mostrar en el mapa la extensión de las áreas que hemos identificado como centros de actividad.

get_hull<- function(df) {
    
    cbind(df$lng, df$lat) %>% 
        as.matrix() %>%
        st_multipoint() %>% 
        st_convex_hull() %>% 
        st_sfc(crs = 4326) %>% 
        {st_sf(categoria = df$categoria[1], cluster = df$cluster[1], geom = .)}
}

hulls <- function(df) {
    
    df %>%
        split(.$cluster) %>% 
        map(get_hull) %>% 
        reduce(rbind)
    
}

mdz_cluster_hulls <- mdz_poi %>%
    filter(cluster != 0) %>%
    select(lng, lat, categoria, cluster) %>% 
    split(.$categoria) %>% 
    map(hulls) %>% 
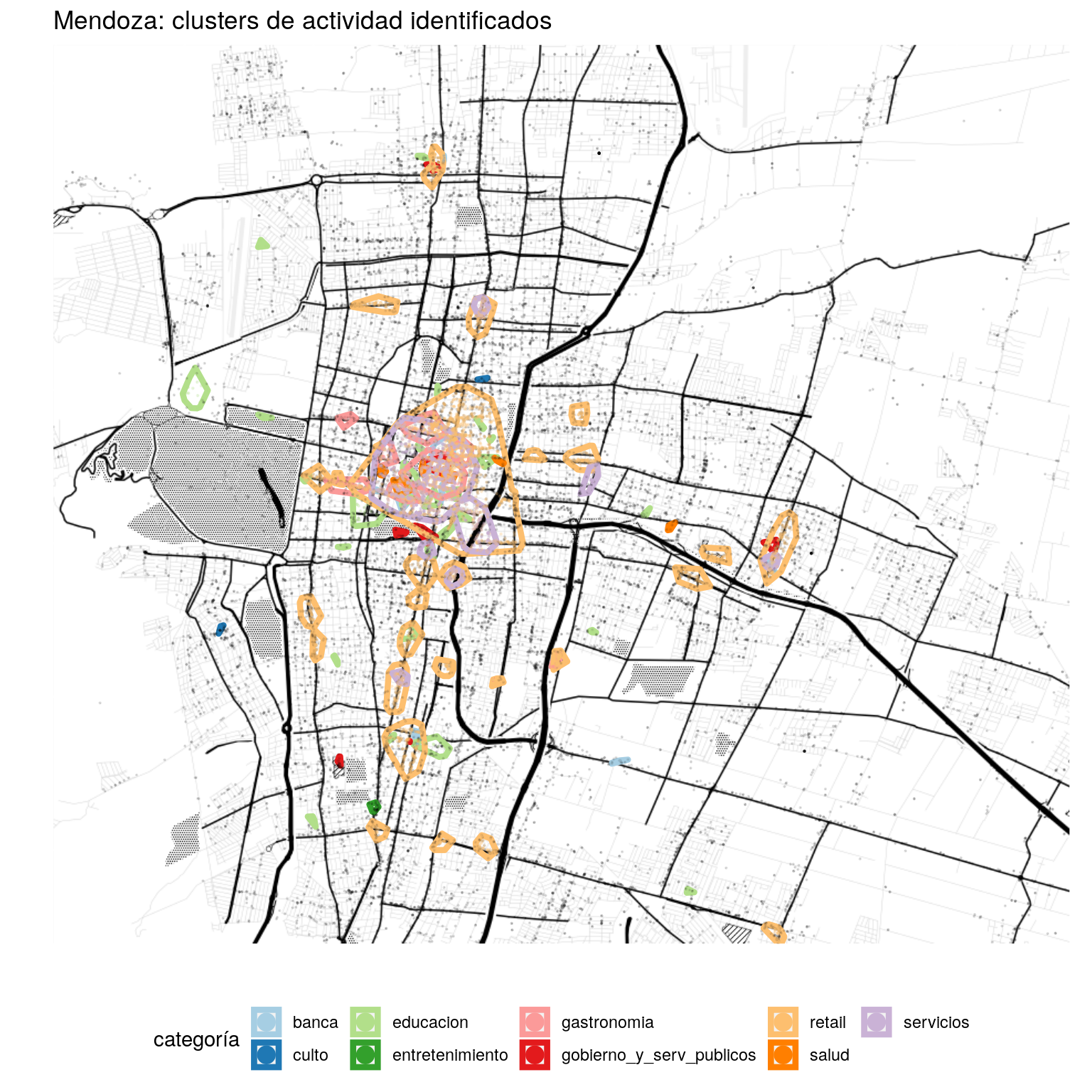
    reduce(rbind)

Lo que hemos obtenido con el paso previo es una serie de polígonos, que representan las envolventes de los clusters que hallamos. Si echamos un vistazo, notamos que la venta al público (retail) es la actividad dominante, seguida de servicios -muy razonable.

ggplot(mdz_cluster_hulls) + 
  geom_sf(aes(fill = categoria), alpha = .7, color = NA)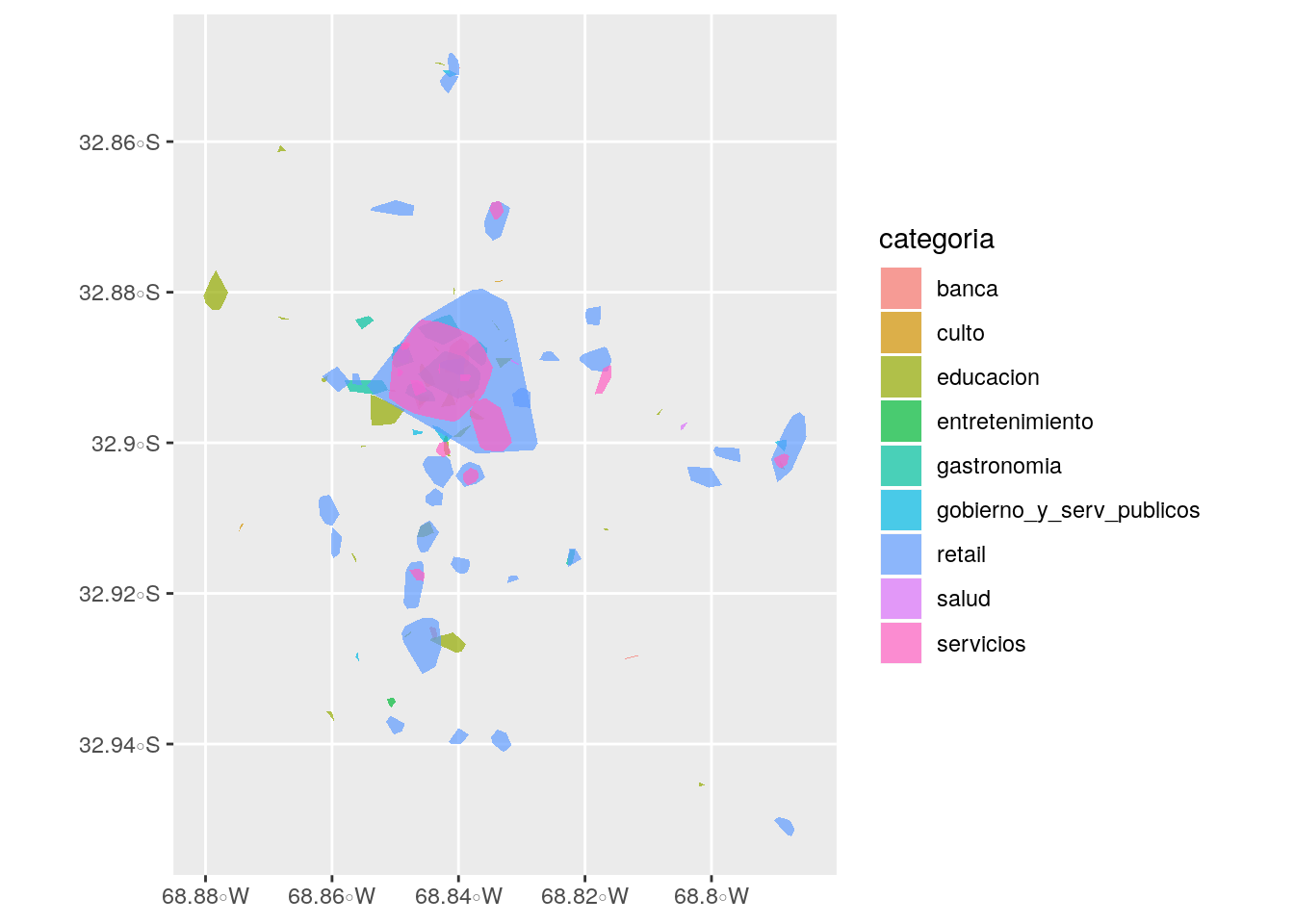

Y por último, todos los ingredientes previos -mapa base, PoI, clusters, envolventes- en una visualización:

#Para reducir la cantidad de etiquetas
hulls_por_cat <- mdz_cluster_hulls %>% 
    group_by(categoria) %>% 
    summarise()

# A graficar

ggmap(mendoza) + 
  coord_sf(crs = st_crs(3857)) + # Necesario cuando se combinan ggmap y geom_sf
    geom_sf(data = hulls_por_cat, fill = NA, size = 1.5, alpha = .5,
            aes(color = factor(categoria)), inherit.aes = FALSE) +
    geom_point(data = filter(mdz_poi, cluster == 0), size = .1, alpha =.1,
               aes(x = lng, y = lat)) +
    geom_point(data = filter(mdz_poi, cluster != 0), size = .2, alpha =.2,
               aes(x = lng, y = lat, color = factor(categoria))) +
    # definimos la escala de colores 
    scale_color_brewer(palette = "Paired") +
    labs(y = "", x = "",
         title="Mendoza: clusters de actividad identificados",
         color = "categoría") +
    # Eliminamos las etiquetas de latitud y longitud de los ejes 
    theme(axis.text.x = element_blank(),
          axis.text.y = element_blank(),
          axis.ticks = element_blank()) +
    guides(colour = guide_legend(override.aes = list(size=4, alpha = 1))) +
    theme(legend.position="bottom")

R DBSCAN